O Último Teorema de Fermat
A história da busca pela demonstração para o Último Teorema de Fermat ilustra a persistência e o rigor que caracterizam a ciência Matemática. A jornada de Andrew Wiles, com seus erros e acertos, demonstra a natureza desafiadora e complexa da pesquisa em matemática. A resolução do Último Teorema de Fermat representou um marco histórico na matemática, coroando uma busca de mais de 350 anos.
Mas como começou essa incrível história? Vamos voltar um pouco no tempo. Pierre de Fermat (1601-1665) foi, na opinião de muitos especialistas, o maior dos matemáticos amadores. De grande saber jurídico e cultura clássica, exerceu altos cargos na administração pública francesa, alcançando o posto de Conselheiro do Parlamento de Toulouse, onde permaneceu até a morte. Boa parte de sua obra matemática é conhecida por sua correspondência, na qual frequentemente apresentava teoremas de sua autoria, sem, no entanto, fornecer suas demonstrações. Em outras ocasiões, anotava esses desafiadores teoremas nas margens dos livros que lia. Alguns deles eram propostos como desafios a outros matemáticos, o que era uma prática comum na época. Fermat se interessou pela matemática ao ler uma tradução da obra de Diofanto (matemático grego que viveu por volta do século III d.C), apaixonando-se pela teoria dos números. Alguns dos teoremas que ele formulou só foram demonstrados décadas após sua divulgação.

Pode-se dizer que, junto com Blaise Pascal, Fermat foi o fundador da teoria das probabilidades. Também contribuiu com Bernoulli na criação do cálculo das variações. Como matemático amador é correto afirmar que ele se satisfazia profundamente com o prazer da descoberta.
Na margem do livro estava escrito
O famoso “Último Teorema de Fermat” é assim chamado por ser a única proposição de Fermat que, até recentemente, resistiu a todas às tentativas de demonstração. Foram cerca de 350 anos de tentativas fracassadas por matemáticos do mundo todo. Aparentemente simples, o teorema de Fermat afirma que a equação
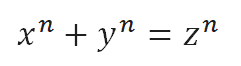
não possui soluções com e inteiros positivos quando o expoente é um número natural superior a 2. Fermat anotou esse teorema na margem da página de um livro, acrescentando que havia encontrado uma prova elegante e concisa que, por ser muito extensa, não caberia no espaço ali disponível. Por “prova”, entende-se uma demonstração geral que se aplica a todos os casos do teorema, não apenas à verificação específica para expoentes particulares. Acredita-se hoje que, se Fermat fez uma demonstração para o seu teorema, ela estava errada. Assim, iniciou-se uma verdadeira busca por uma demonstração geral, bem como por soluções para casos específicos. O próprio Fermat registrou uma solução para o caso.
O impulso de Fermat para a matemática
Na década de 1840, Ernst Eduard Kummer iniciou o estudo do que hoje se chama teoria dos números algébricos, que possibilitou a demonstração do Último Teorema de Fermat para um grande número de expoentes, segundo B. Cipra (“Science”, 261, 32). Com o auxílio de computadores modernos, chegou-se a incluir todos os expoentes até 4 milhões. Durante esse esforço, várias teorias novas surgiram, enriquecendo diversos campos da matemática, principalmente a Álgebra. Em 1988, o anúncio de Yoichi Miyaoka de que havia conseguido provar o Último Teorema de Fermat causou grande sensação. No entanto, especialistas encontraram muitas falhas em sua suposta prova.
Andrew Wiles, na década de 1990, seguiu um caminho diferente de seus antecessores, apresentando sua prova em três conferências consecutivas, a partir de um teorema demonstrado por Ken Ribet, que por sua vez se baseou em uma ideia desenvolvida por Gerhard Frey. Este havia declarado que um importante problema da teoria das curvas elípticas, que descreve propriedades de curvas através de equações e vice-versa, poderia abrir caminho para a solução do teorema de Fermat. Esse problema é conhecido como “conjectura de Taniyama-Weil”, de grande importância desde a década de 1950.

Em sua série de conferências, Wiles, em cerca de 200 páginas, resolveu a conjectura, segundo a revista Science, demonstrando que ela se aplica a uma classe infinita de curvas elípticas. Na opinião de muitos matemáticos presentes nas reuniões realizadas no Instituto Newton de Cambridge, Reino Unido, de 21 a 23 de junho de 1993, o teorema de Fermat seria apenas um corolário dos resultados obtidos por Wiles. Esse fato ilustra a grandeza do trabalho realizado por Wiles. O mundo parecia não acreditar que finalmente a busca por uma demonstração para o último teorema de Fermat havia chegado ao fim.
Erro quase fatal
Logo em seguida ao anúncio da conferência, notícias recentes publicadas pela revista americana “Time” davam conta de que os matemáticos encarregados de analisar a prova havia encontrado um erro no trabalho de Wiles. O famoso teorema permanecia, portanto, sem solução.
A prova original de Wiles, apresentada em 1994, tinha uma falha significativa que foi descoberta durante a revisão por pares. No entanto, Wiles e Taylor (ex- aluno de doutorado de Wiles) trabalharam juntos por meses para corrigir essa falha. Finalmente, em julho de 1995, surgiram notícias de que a prova apresentada por Wiles estava correta e o Último Teorema de Fermat finalmente demonstrado. A resolução do Último Teorema de Fermat por Wiles representou um marco histórico na Matemática, coroando uma incansável busca de mais de 350 anos.
Reconhecimento
Por esse incrível trabalho sobre o Último Teorema de Fermat Andrew Wiles recebeu diversos prêmios e honrarias. Alguns dos prêmios mais notáveis incluem Prêmio Abel (2016): concedido pela Academia Norueguesa de Ciências e Letras, é considerado o mais prestigioso prêmio em matemática; Medalha Copley (1997): concedida pela Royal Society, é uma das mais antigas e prestigiadas premiações científicas do Reino Unido; Prêmio Shaw em Ciências Matemáticas (1996): concedido pela Fundação Shaw, é um importante prêmio internacional. Além de outros prêmios como Prêmio Whitehead (1988), Prêmio Fermat (1995), Prêmio Rolf Schock de Matemática (1995), Prêmio Ostrowski (1995), Prêmio Wolf de Matemática (1995/1996), Medalha Real (1996), Prêmio de Matemática NAS (1996), Prêmio Cole (1997), Clay Research Award (1999), Prêmio Pitágoras (2004) e Medalha De Morgan (2019).
O reconhecimento público da conquista de Wiles demonstra a importância e o impacto de seu trabalho na Matemática e na ciência como um todo.
